概要
業務でモンテカルロ法を使う事があった際、会社のつよつよさんに
「乱数発生させるときは、ラテン超方格法を利用すると精度が上がるよ」
というアドバイスをもらったので、実装してみました。メモとして残します。
ラテン超方格法について
何それ
ややこしい数式は避けて、概要だけまとめます。
- 多変数の層別サンプリング手法のひとつだよ
- 一様分布に比べて偏りが少ないから、少ないn数で精度が出せるよ。
- 実験計画法などでよく利用されているよ。
なお、ラテン超方格法の説明についてはこちらの記事を参考にしてます。
図で理解する
一般的な一様分布は決められた範囲内を疑似乱数を発生させてサンプリングを行いますが、ラテン超方格法は下記の手順で乱数を発生させます。
- 範囲内をグリッドで区切る
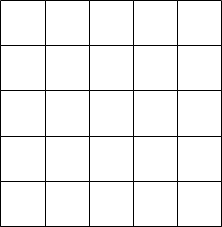
- 列から行がかぶらないように1列づつグリッドを選択
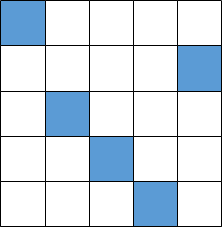
- グリッド内で乱数発生
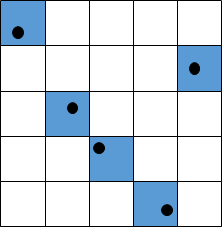
なるほど、この方法ならよりばらつきが少なくサンプルが取れそう。
円周率近似実装
ということで実装して精度検証してみます。
精度検証の方法は下記のnishipyさんの記事を参考に、モンテカルロ法を用いた円周率近似を用いて一様分布とラテン超方格法の場合で比較をしていきたいと思います。

下記の手順で円周率の近似は行います。
- 0~1の範囲で乱数を発生させる。(ラテン超方格法 or 一様分布)
- 円の四分の一のサイズの半径1の扇型を描画し、扇形の外にある点の個数と内側にある個数をカウント
- (扇形の中にある点の個数/全部の点の個数)×4 で円周率を計算
ラテン超方格法
まずはラテン超方格法を実装します。なお、あらかじめpyDOE2のpip installは必要なので済ませてください。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
import pyDOE2 as doe from sklearn.preprocessing import MinMaxScaler import pandas as pd #レンジの設定 boundary = pd.DataFrame({'x':[0,1],'y':[0,1]}) # 1000サンプル作成 lhs = doe.lhs(2, samples=1000, criterion='center',random_state=1) scaler = MinMaxScaler() min_max = scaler.fit(boundary) #プロット value = pd.DataFrame(min_max.inverse_transform(lhs), columns=boundary.columns) value.plot.scatter(x='x', y='y') |
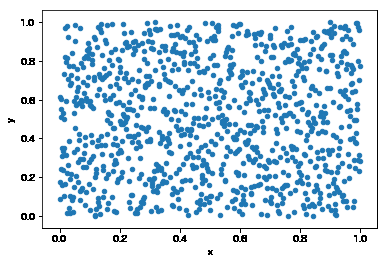
まずはサンプル数1000で実装しました。ぱっと見普通の乱数と変わらなそう。
次に原点からの距離を計算して、各店が円の内側にあるか、外側にあるかを判定します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
import math n_in = 0 n_out = 0 x = value['x'] y = value['y'] #中心からの距離が1よりも大きいかどうかで場合分け for i, j in zip(x, y): if math.hypot(i, j) < 1: n_in += 1 else: n_out += 1 print("内: {} 個".format(n_in)) print("外: {} 個".format(n_out)) |
|
1 2 3 |
#出力結果 内: 792 個 外: 208 個 |
円の内外の判定ができたので、最後に円周率を計算します。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
l = np.linspace(0, 1, 100) plt.plot(l, np.sqrt(1-l**2)) plt.gca().set_aspect('equal', adjustable='box') plt.xlabel("x") plt.ylabel("y") plt.fill_between(l,0,np.sqrt(1-l**2),facecolor='b',alpha=0.5) plt.plot(x, y, 'o', markersize=0.4, label="random plot") plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left') #プロットが扇形部分どれだけ入っているか判定 pi_closed = 4 * n_in / (n_in + n_out) print("円周率近似値: {:.3f}".format(pi_closed)) |
|
1 2 |
#出力結果 円周率近似値: 3.168 |
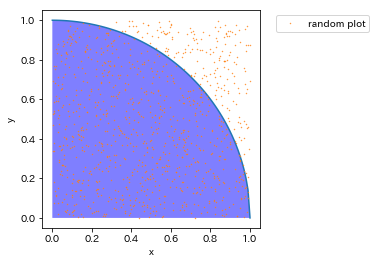
円周率の近似値は3.168になりました。
サンプル数1000にしてはそこそこ精度があるのではないでしょうか?
一様分布
比較のため、一様分布を使って円周率の計算をしてみます。
|
1 2 3 4 5 6 7 |
import numpy as np import matplotlib.pylab as plt x = np.random.rand(1000) y = np.random.rand(1000) value2 = pd.DataFrame({'x':x,'y':y}) value2.plot.scatter('x','y') |
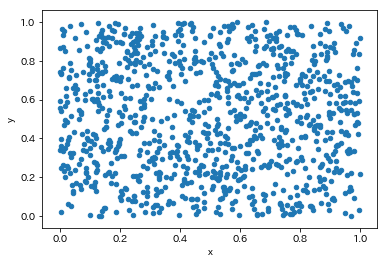
ぱっと見はラテン超方格法と変わりないですが、よく見ると粗密の塊がラテン超方格法よりも多い気もします。
あとは先ほどと同様の処理をして円周率を近似します。コードは前節と同じなので詳細は割愛します。
|
1 2 3 |
#一様分布の円周率近似値 pi_closed = 4 * n_in / (n_in + n_out) print("一様分布 円周率近似値: {:.3f}".format(pi_closed)) |
|
1 2 |
#出力結果 一様分布 円周率近似値: 3.268 |
近似値が3.268であったので、ラテン超方格法の方が精度が高いということがわかります。
サンプル数変更して精度確認
最後にサンプル数を変更した結果を下記に示します。サンプル数上げるとどちらも精度が上がっていきますが、全体的な精度はラテン超方格法の方が高いです。
| サンプル数 | ラテン超方格法 円周率近似値 | 一様分布 円周率近似値 |
| 100 | 3.200 | 3.080 |
| 1000 | 3.168 | 3.268 |
| 10000 | 3.136 | 3.128 |
| 100000 | 3.143 | 3.144 |
まとめ
ラテン超方格法、少ないサンプルでも精度が出るので、興味あれば使ってください。
参考文献





コメント